

#All trigonometric identities formulas plus
The difference formula for tangent states that the tangent of the difference of two angles equals the difference of the tangents of the angles divided by 1 plus the product of the tangents of the angles. The sum formula for tangent states that the tangent of the sum of two angles equals the sum of the tangents of the angles divided by 1 minus the product of the tangents of the angles.The sum and difference formulas for sine and cosine can also be used for inverse trigonometric functions.The difference formula for sines states that the sine of the difference of two angles equals the product of the sine of the first angle and cosine of the second angle minus the product of the cosine of the first angle and the sine of the second angle. The sum formula for sines states that the sine of the sum of two angles equals the product of the sine of the first angle and cosine of the second angle plus the product of the cosine of the first angle and the sine of the second angle.The sum and difference formulas can be used to find the exact values of the sine, cosine, or tangent of an angle.Trigonometric identities of the sum and difference of two angles. Following are the topics covered in the pdf.
#All trigonometric identities formulas download
Click the link below and download the pdf. The difference formula for cosines states that the cosine of the difference of two angles equals the product of the cosines of the angles plus the product of the sines of the angles. Here is the compilation of all trigonometric formulas.

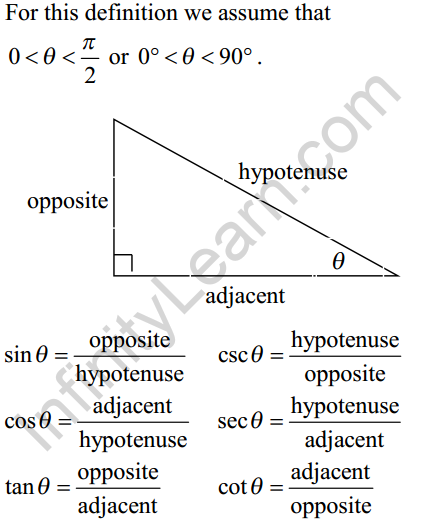
These are special equations or postulates, true for all values input to the equations, and with innumerable applications. The trigonometric identities we will examine in this section can be traced to a Persian astronomer who lived around 950 AD, but the ancient Greeks discovered these same formulas much earlier and stated them in terms of chords. The trigonometric identities, commonly used in mathematical proofs, have had real-world applications for centuries, including their use in calculating long distances. Using the definitions of sine and cosine, we will learn how they relate to each other and the unit circle.How can the height of a mountain be measured? What about the distance from Earth to the sun? Like many seemingly impossible problems, we rely on mathematical formulas to find the answers. The Pythagorean identities can be used to simplify problems by transforming trigonometric expressions, or writing them in terms of other trigonometric functions.The three identities are \cos^2 t + \sin^2 t = 1, 1 + \tan^2 t = \sec^2 t, and 1 + \cot^2 t = \csc^2 t.The Pythagorean identities are derived from the Pythagorean theorem, and describe the relationship between sine and cosine on the unit circle.The Pythagorean identities are useful in simplifying expressions with trigonometric functions. Note that we now have enough information that we could use the Law of Sines to solve for the unknown angles \alpha and \gamma in the triangle. In turn, these trigonometric functions are defined using the sides of the right triangle, that is, the opposite side, the adjacent side, and the hypotenuse. The law of sines states that the following proportions are equal: \displaystyle All trigonometric identities are derived from the six fundamental trigonometric functions, which are sine, cosine, tangent, cosecant, secant, and cotangent.The law of sines is used to find the measurements of all three angles and all three sides in a triangle.


 0 kommentar(er)
0 kommentar(er)
